J'ai effectué
mon stage de 3ème année de l'Ecole des Mines d'Alès
sous la direction d'Antoine Labeyrie au LISE (Laboratoire d'Interférométrie
Stellaire et Exoplanétaire) situé sur le site de l'Observatoire de Haute Provence à St Michel l'Observatoire. Pendant ce stage
j'ai principalement travaillé sur une application qui réalise
une analyse de front d'onde selon la méthode que je vais détailler
sur cette page, appliquée à un télescope de type "boule"
avec un miroir mince de 143 mm de diamètre qui sera intégré
dans un futur projet d'interféromètre géant : le projet
OVLA (Optical Very Large Array).

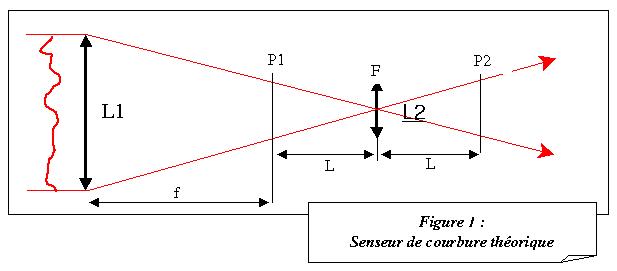
Les données de
départ d'un « senseur de courbure » sont en fait un
jeu de 2 images prises par une caméra CCD de part et d'autre du
plan focal de l'objectif (dans notre cas, le miroir primaire du télescope)
que l'on veut tester. La figure 1 vous présente le cas théorique
de ce senseur : on mesure en fait 2 distributions d'intensité I1
et I2 dans les plans P1 et P2.
Sous réserve
de certaines hypothèses particulières que je ne présenterai
pas, la différence normalisée entre les 2 intensités
dans les plans P1 et P2 est donnée par la relation suivante :
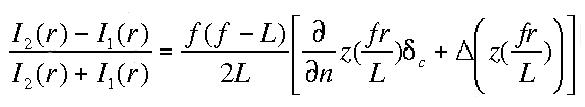
Où delta minuscule est une impulsion de Dirac sur le contour de la pupille, pondérée par la pente radiale du front d'onde et où delta majuscule représente le Laplacien du front d'onde, c'est à dire sa courbure.On peut astucieusement résoudre cette équation en remarquant qu'en passant dans le domaine de Fourier, l'opérateur Laplacien revient à faire une multiplication par u²+v² si les variables u et v sont celles de Fourier en 2D.
Ainsi, on calcule la différence normalisée des 2 images intra et extra-focales, on en prend la transformée de Fourier, on divise par u²+v² en prenant garde au point (0,0) et on fait la transformée inverse pour remonter au front d'onde. Cette approche simple marcherait avec un front d'onde qui n'aurait pas de limites (dans ce cas, le d est toujours nul). En réalité, le Laplacien du front d'onde est multiplié par PSF (Point Spread Function) P(x,y) c'est à dire la fonction de transfert de la pupille d'entrée ce qui revient à dire que sa transformée de Fourier est convoluée par la transformée de Fourier de cette fonction P(x,y).
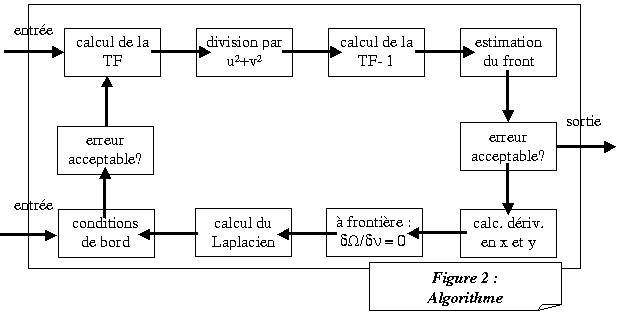
Une méthode utilisable pour faire intervenir ces conditions aux limites est d'extrapoler le front d'onde au delà des frontières du domaine et de s'arranger pour que la courbure radiale soit nulle dans une bande la plus mince possible autour de la frontière définissant la pupille. On peut ensuite une fois cette astuce appliquée, recalculer la transformée inverse du front calculé et estimer l'erreur commise. La figure 2 résume le déroulement de l'algorithme.
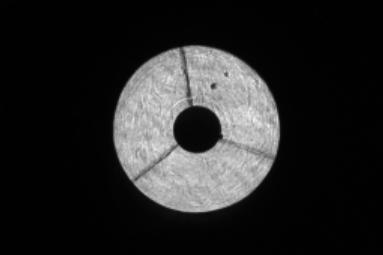
La figure 3 présente 2 images types intra et extra-focales prises avec une caméra ST7 à l'intérieur du télescope « boule ».
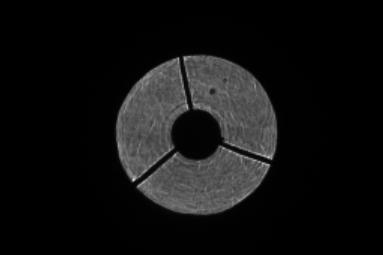
Le résultat
de cet algorithme est un front d'onde reconstruit, lui aussi exportable
sous forme d'une image FITS dont un exemple est illustré par la
figure 4 qui suit :

On a en quelque sorte réalisé une pseudo boucle d'asservissement relativement lente car il faut environ 1 minute entre l'acquisition des images, la lecture de la CCD, l'analyse de surface d'onde et l'application des commandes aux actionneurs qui permet d'exploiter au mieux les possibilités du télescope puisque les défauts de l'image dus à la turbulence deviennent prépondérants sur ceux de liés à la qualité de l'optique.
On peut cependant appliquer un traitement supplémentaire assez simple mais en même temps très intéressant qui consiste à projeter le résultat (correctement échantillonné) sur une base classique de polynômes : celle de Zernike.
Ces polynômes ont en effet l'énorme intérêt de constituer une base orthogonale de l'ensemble des déformations d'une surface décrite par ses variables polaires et d'avoir une expression analytique, ainsi que leur transformée de Fourier. Ils sont en fait bien connus des opticiens et des mathématiciens mais également du grand public mais sous des noms plus parlant d'astigmatisme, de coma ou de trèfle.
Le front d'onde s'écrit donc de la façon suivante :
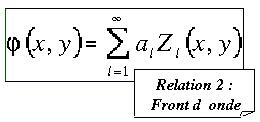
Ces polynômes s'expriment généralement en fonction de leur degré radial n et de leur degré azimutal m comme indiqué dans la relation 3 :
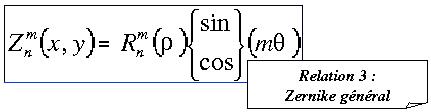
où (rho,theta) sont les coordonnées polaires associées à (x,y) et R un polynôme de degré n ne contenant pas de puissance inférieure à m :
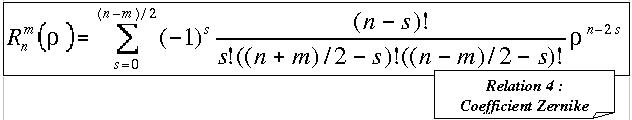
Pour un degré n, on a tous les degrés azimutaux compris entre 0 et n et dont la parité est la même que celle de ce degré radial. Un degré azimutal comprend en fait 2 polynômes, un en cosinus et l'autre en sinus. (voir tableau 1).
Les degrés radial et azimutal d'un polynôme de Zernike nous renseignent sur les fréquences spatiales maximales de celui-ci, par rapport à, respectivement ces coordonnées radiales et angulaires. On admet d'ailleurs que le nombre de polynômes de Zernike nécessaire pour la commande d'un miroir déformable est approximativement égal à son nombre d'actionneurs, car ils traduisent un même nombre de fréquences spatiales.
Le tableau 1 présente les expressions des 15 premiers polynômes de Zernike en fonction de leur degré radial (n) et azimutal (m) :

On peut ainsi en exprimant le front d'onde comme une combinaison linéaire de ces polynômes quantifier avec précision les défauts dont souffre l'optique de l'instrument sur lequel est faite cette analyse. Pour l'optique active où les défauts sont d'ordre faible, les polynômes de Zernike suffisent à décrire convenablement les aberrations d'un système optique.
Ce sont les coefficients al de la relation 2 qui sont les résultats de l'analyse de front d'onde réalisée par notre logiciel. Ce sont ces coefficients que nous passons au programme de contrôle du barillet actif du télescope, afin qu'il calcule les forces à appliquer sur les actionneurs contrôlant les déformations du miroir.
La figure 5 présente l'amélioration apportée aux images en montrant 2 images de l'étoile polaire avant et après correction par le logiciel d'analyse de front d'onde.

La largeur de la tâche d'intensité moyenne est avant correction d'approximativement 30 secondes d'arc alors que celle de l'image après correction est comprise entre 3 et 5 secondes d'arc, la turbulence atmosphérique à l'OHP étant rarement inférieure à cette valeur.
La boucle de contrôle complète remplit donc bien son office en permettant à un miroir de 24 mm d'épaisseur de verre ordinaire d'avoir des performances comparables à celles de miroirs beaucoup plus épais ? bien entendu plus chers à réaliser à même diamètre (143 mm) mais en même temps impossibles à utiliser dans des télescopes qu'on déplace pour faire de l'interférométrie avec des bases importantes.